Problem

• Given an image, what is foreground and what is background ?
• E.g: Hockey puck against the ice, football against the field
• If (x,y) is a foreground pixel, then nearby are also likely foreground.

For each pixel i:

• $a_i$ = likelihood that pixel i is in foreground
• $b_i$ = likelihood that pixel is in background

How these values are generated depends on the application.

⇒ if $a_i > b_i$ then we make $i$ a foreground pixel.

Noted that foreground pixels tend to be near to one another, and background pixels tend to near one another.

We represent an image as a graph G(V,E):

• V contains a vertex for each pixel

• E contains an edge between pixels $i$ and $j$ if $i$ and $j$ neighbor each other.

  

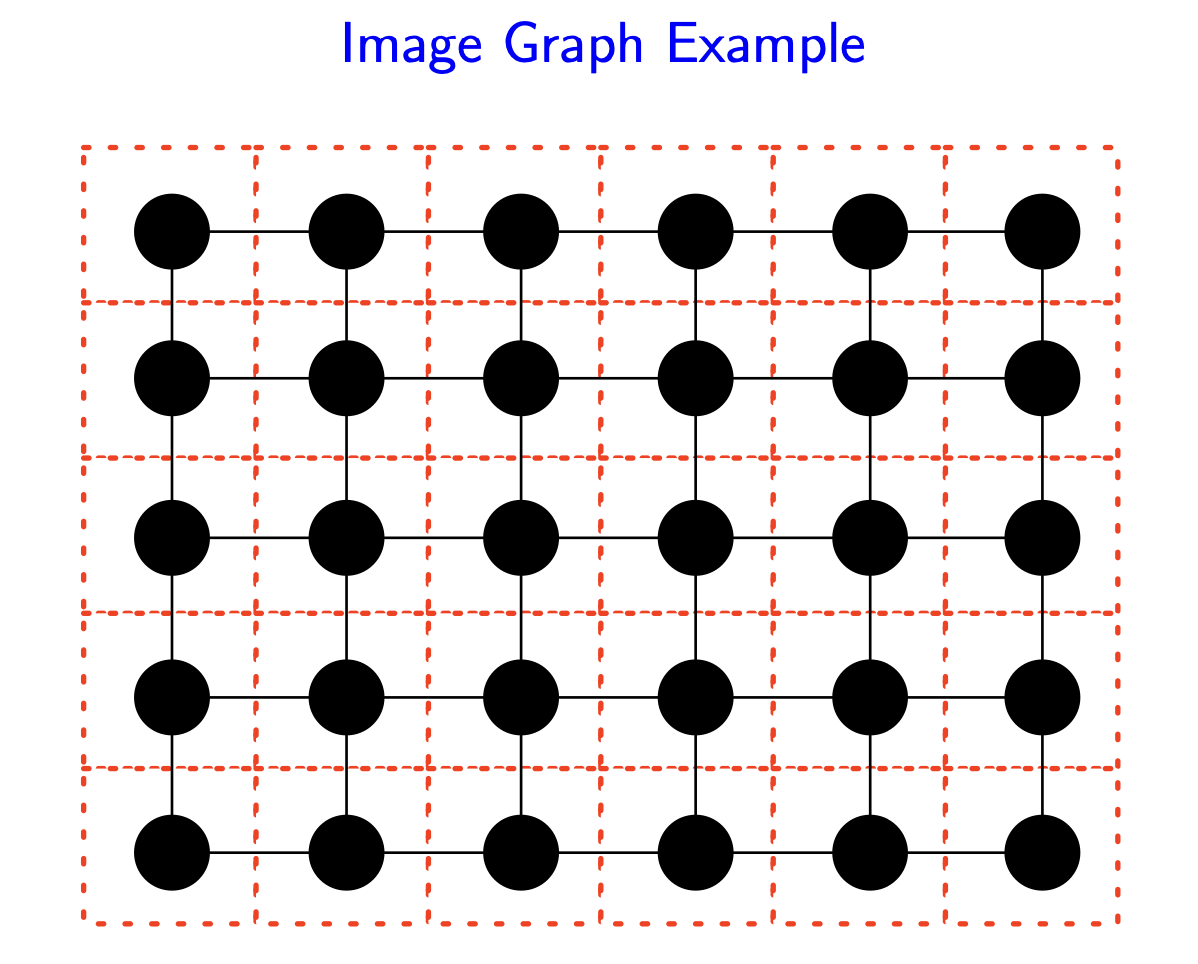
Modeling the problem

For every neighboring pair of pixels {i,j}, we have a parameter $p_{ij}$ = the penalty for puttinh one of $i,j$ in foreground and the other in the background.

Objective :

Partition the set of pixels into 2 sets $A$ and $B$ to maximize:

\[q(A,B) = \sum_{i\in A}a_i + \sum_{j\in B}b_j - \sum_{(i,j)\in E ; i≠j}p_{ij}\]

Review Min-Cut and compare to Image Segmentation

Minimum cut : Partition of vertices of a directed graph into 2 sets A,B, with $s\in A,t\in B$ to minimize weight of edges crossing from $A$ to $B$.

Image segmentation: Partition the vertices of the image graph into 2 sets A and B to maximize $q(A,B)$

Differences:

• Maximization vs minimization
• Image segmentation graph has no sink or source , and undirected
• Image segmentation has a more complicated objective function $q(A,B)$ with weights on the nodes

Solution

??? HOW TO MAKE IT POSSIBLE ???

IMAGE SEGMENTATION INSTANCE -> MIN-CUT

Missing source and sink ?

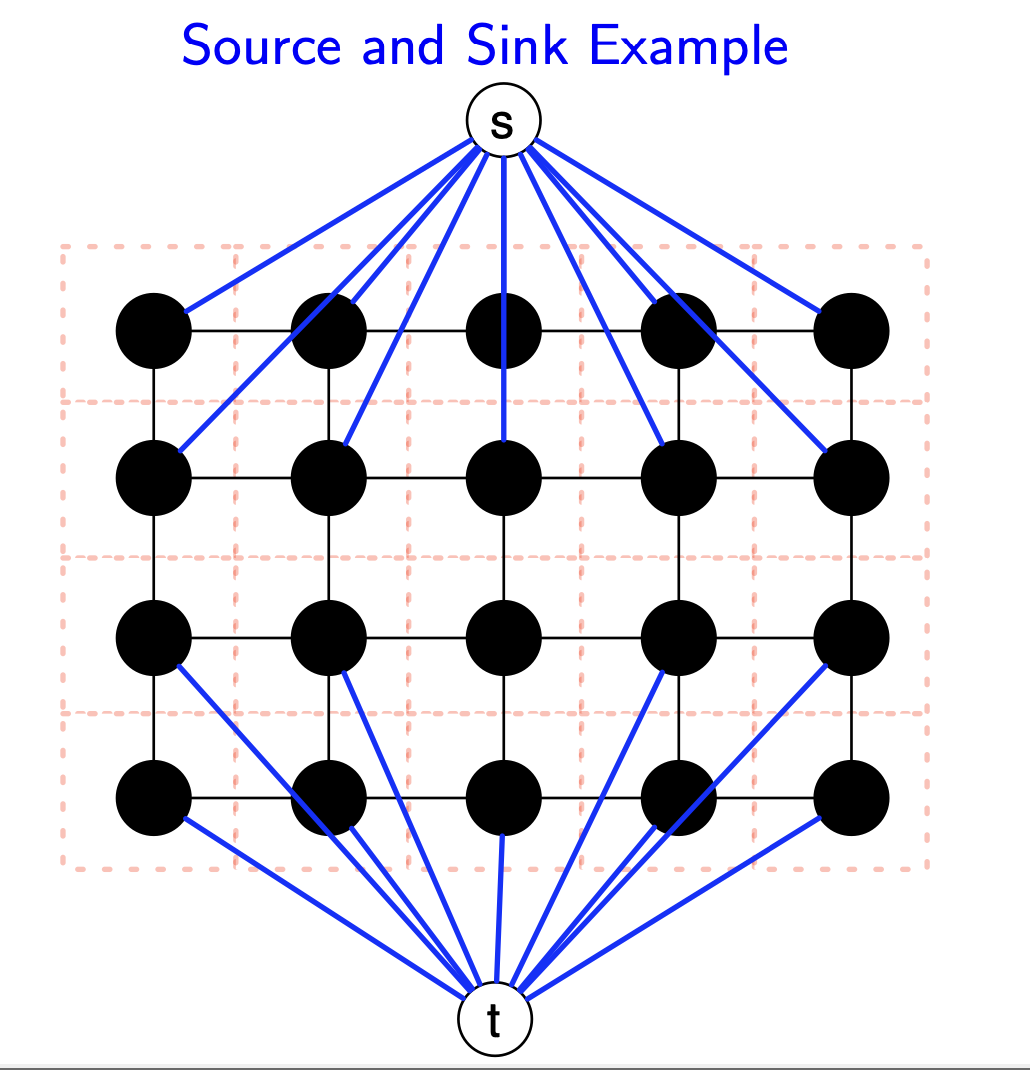
Adding:

• a source s with an edge $(s,u)$ for every vertex $u$.
• a sink $t$ with an edge $(u,t)$ for every vertex $u$.

Small fact: s will represent the foreground, and t will represent the background

Handle directed edges

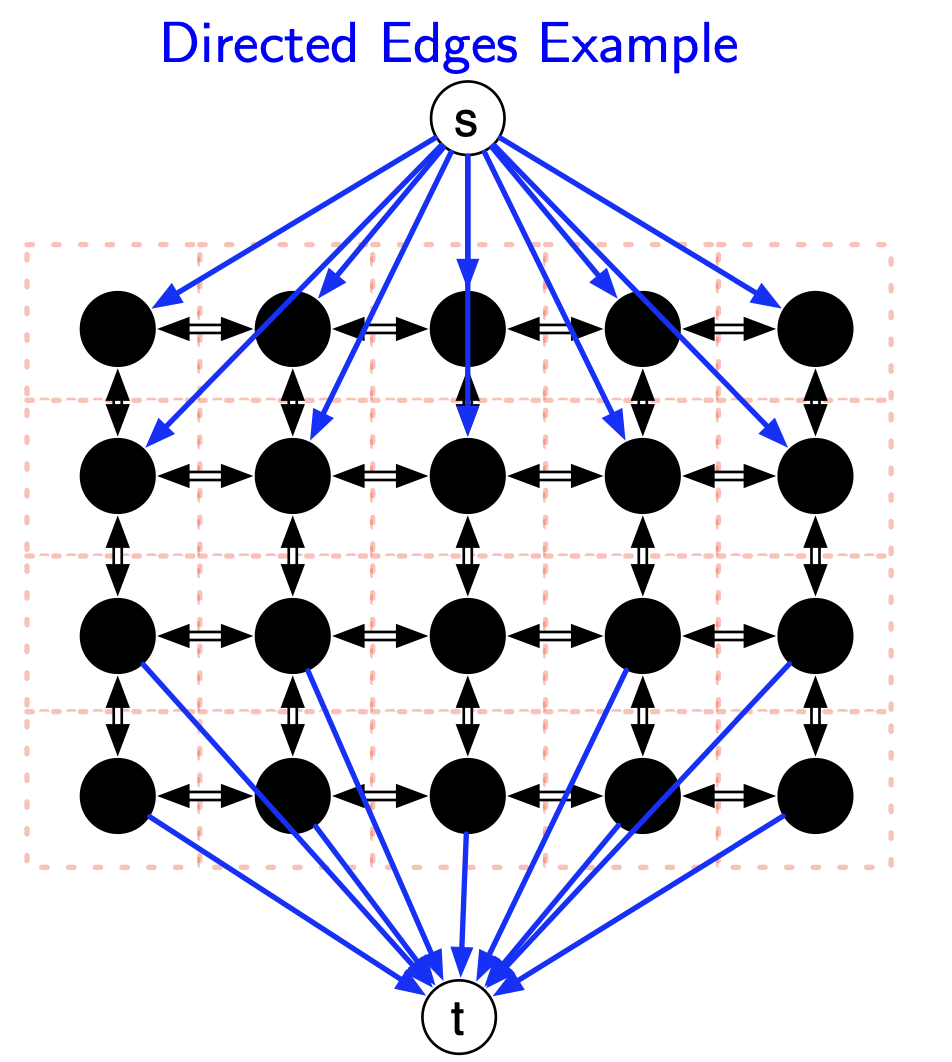
Convert the current undirected graph into a directed graph:

• Edges adjacent to $s$ are directed so they leave $s$.
• Edges adjacent to $t$ are directed so they enter $t$.
• All other edges are replaced by 2, anti-parallel edges

Last issue: How do we handle the parameters $a_i,b_j,p_{ij}$ and minimization vs maximization ?

Maximization → Minimization

Let $Q = \sum_i(a_i+b_i)$

Old objective function was to maximize:

\[q(A,B)=\sum_{i\in A}a_i + \sum_{j \in B}b_j - \sum_{(i,j)\in E;i≠j} p_{ij}\]

We want to maximize:

\[q(A,B) = Q - \sum_{i\in A}b_i - \sum_{j\in B}a_j - \sum_{(i,j)\in E; i≠j}p_{ij}\]

This is same as minimize:

\[q'(A,B) = \sum_{i\in A} b_i + \sum_{j\in B} a_j + \sum_{(i,j)\in E;i≠j}p_{ij}\]

Voila! we did convert it into the problem of min-cut with modified graph G (adding source $s$ and sink $t$)

Summary

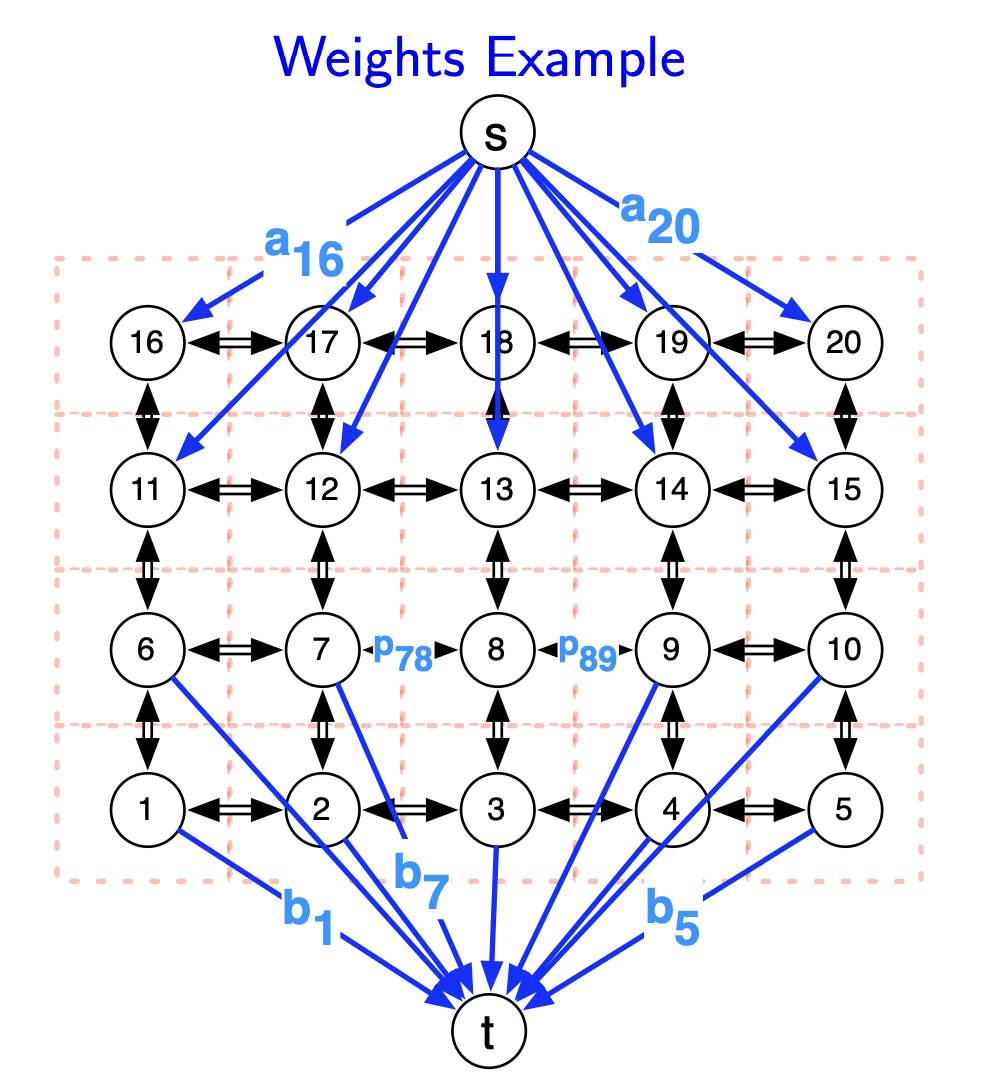
We use the parameters $a_i,b_i,p_{ij}$ as weights on the various edges:

• Edges between 2 pixels $i$ and $j$ get weight $p_{ij}$
• Edge $(s,i)$ gets weight $a_i$
• Edge $(j,t)$ gets weight $b_j$

⇒ The capacity of an $s-t$ cut $(A,B)$ will equal the quantity we’re trying to minimize

We’ve designed the graph so that the capacity of an s-t cut (A,B) equals the quality of the partition defined by taking:

• A: the set of foreground pixels (plus s)
• B: the set of background pixels (plus t)

---