Introduction
Natural agent excel at discovering pattern, extracting knowledge and performing complex reasoning based on the observed data
⇒ How to build AI systems to do the same ?
- View the world under the lens of probability
- Think any observed data set, denoted by $D$ as a finite set of samples from an underlying distribution (usually unknown), say $p_{data}$. The goal of any generative mdoel is to approximate $\hat p_{data}$ ( the estimator of $p_{data}$) give the data set $D$
- Then we can use the learned generative model for downstream task or downstream inference.
Learning
We will parametric-approximate the data distribution, which summarize all the information about the dataset $D$ in a finite set of parameters. Parametric models scale more efficiently with large datasets than non-parametric model but parametric models are limited in the family of distributions they can represent
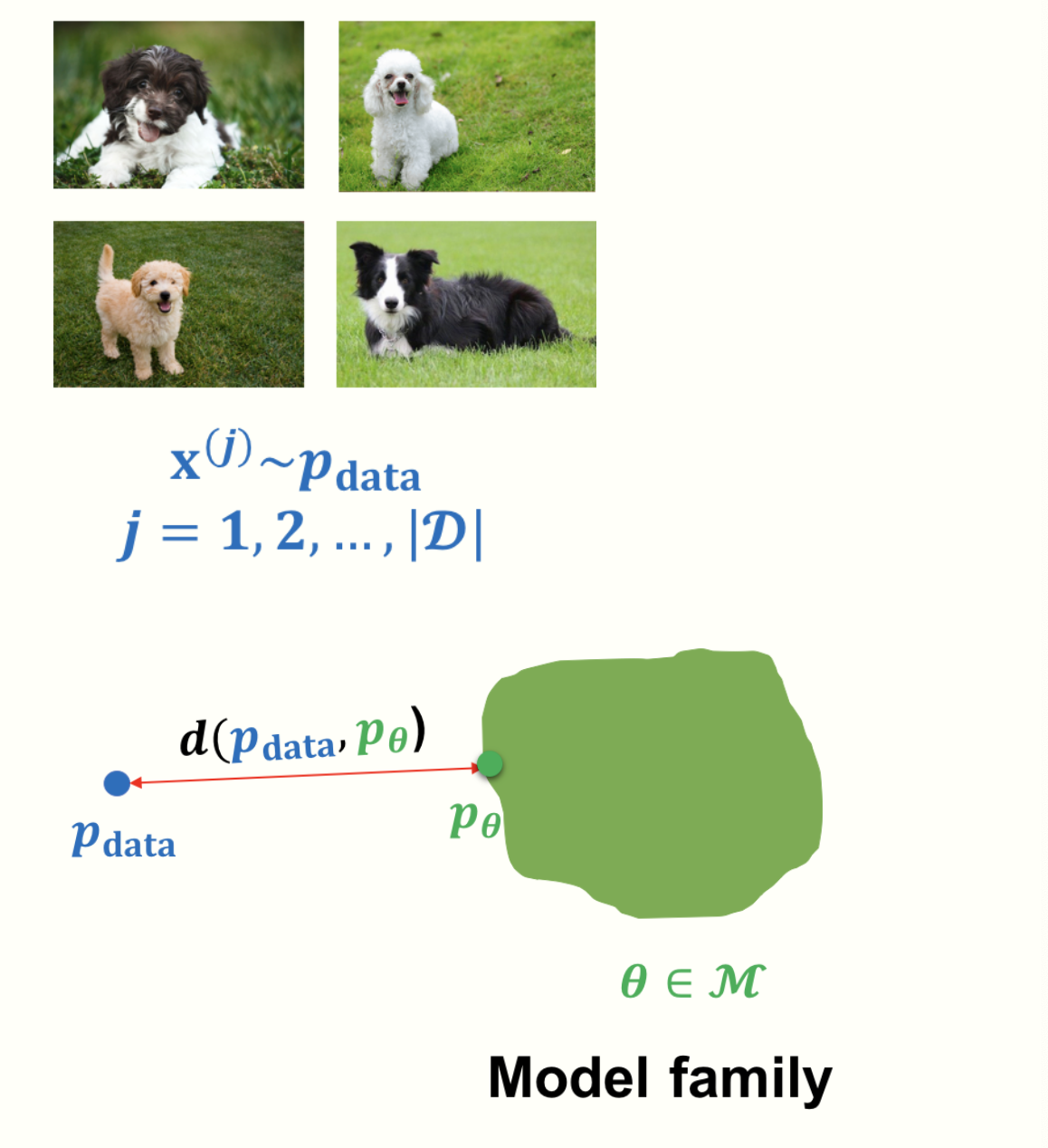
Problem description:
Given dataset $D$ , we aim to learn the parameters $\theta$ of generative model within a model family $M$ such that the distance of the (estimator) model distribution $p_{\theta}$ is as close as possible to the (ground truth) data distribution $p_{data}$.
\[\min_{\theta \in M}d(p_{data},p_{\theta})\]where $p_{data}$ is accessed via dataset $D$ and d(.) is the distance between probability distributions (we can design this metric for each specific problem , one very popular is KL divergent..)
Difficulty
An image from modern phone camera has resolution 700*1400 pixels, with 3 channels of RGB. Hence the number of possible images is more than $10^{8000000}$, which is to large to any machine can handle. Learning a generative model with such a limited dataset is a highly underdetermined problem.
But the world is highly structured and automatically discovering the underlying structure is key to learn a generative model. For example, given just a few images of dogs, we can hope to learn some very most basic features of any dog can have ( 2 ears, fur, nose,eyes, etc…). Instead of inserting the prior knowledge into the model, we want the model to learn this features by itself. Some questions we will primarily interested in:
- What is the representation for the model family $M$ ?
- What is the objective function (or distance function) $d(.)$ ?
- What is the optimization process for minimizing the objective function ?
Inference
As we defined before, Generative models learn a joint distribution over the entire data. But differ from supervised learning models (like logistic regression, etc…)- the models give out the prediction given the input, the generative model can not do like that ( because it has no label or value to predict), so what does it can infer ??
3 inference queries for evaluating generative models:
- Density estimation: Given datapoint x, what is the probability of $p_{\theta}(x)$ ?
- Sampling: How can we generate data from the model distribution, $x_{new} \sim p_\theta(x)?$
- Unsupervised representation learning: How can we learn meaningful feature representations for a datapoint x ? ( This is extremely useful for supervised downstream tasks !!! , we’ll talk about it later in this series of generative model. )