Motivation
Digit-classification problem, with MNIST dataset.
Notation:
- $X_l={(x^{(i)},y^{(i)})}_{i=1}^{100}$: is labeled dataset
- $X_u = {x^{(i)}}_{i=101}^{600}$ is labeled dataset
BUT: only give a labeled dataset with 100 labeled images and 500 images with NO labels. How to build an effective classifier ???
- We can build a classifier only using $X_l$(supervised-learning) (but in the code experiment, only get 75% acc. with simple classifier)
⇒ Want to integrate the huge amount of unlabeled dataset into the model to boost the overall performance.
That’s the motivation for Semi-Supervised Learning !
Latent variable model
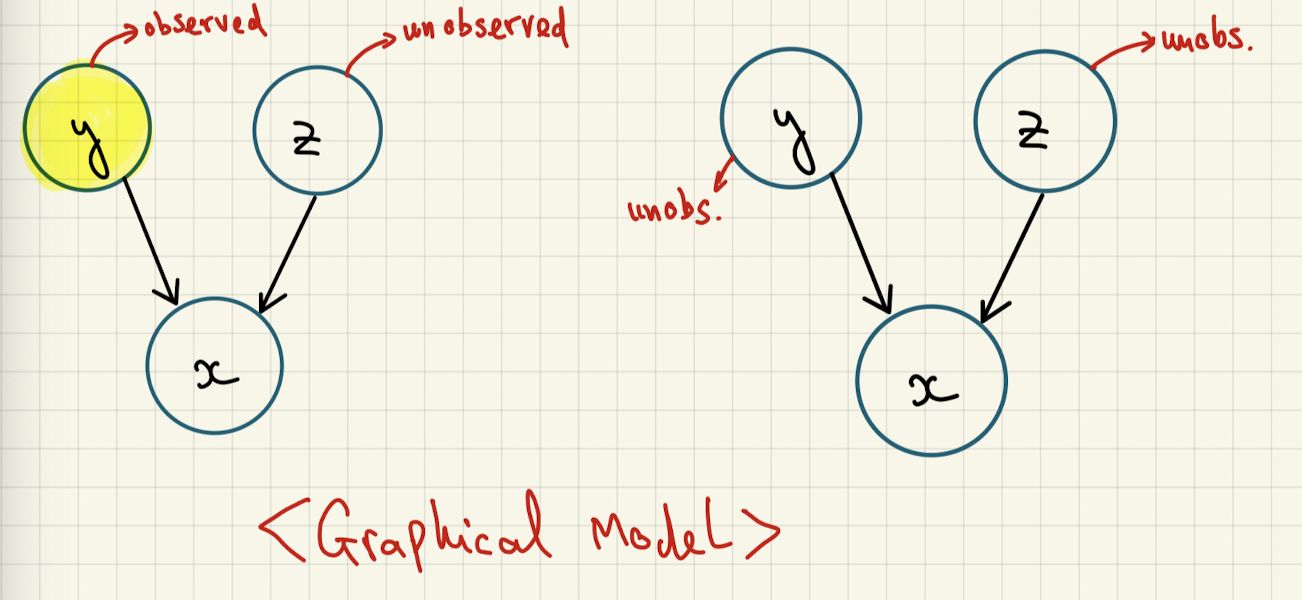
- x: input image
- y: class (a.k.a digit in the image) - partially observed (latent variable)
- z: latent variable (always unobserved)
Log-likelihood
\[\log p_{\theta}(x) = \sum_{x\in X_l}\log p_{\theta}(x) + \sum_{x\in X_l}\log p_{\theta}(x,y)\]where: y is discrete variable ⇒ $\int \rightarrow \sum$
\[p_{\theta}(x) = \sum_{y\in Y} \int p_{\theta}(x,y,z)dz \\ p_{\theta}(x,y) = \int p_{\theta}(x,y,z) dz\]Our goal is to maximize the log-likelihood, but it’s intractable, hence the idea of ELBO ( Evidence Lower Bound ).
Objective (Simpler version of the paper but good enough, acc.$\approx$94%)
\[\max_{\theta,\phi}\sum_{x\in X}ELBO(x;\theta,\phi) + \alpha\sum_{x,y\in X_l}\log q_{\phi}(y|x)\]$\alpha$: weight put on $\log q_\phi(y|x)$ ( this term can be treated as regularization of amortized inference model)
We delve into detail of $ELBO(x;\theta,\phi)$:
\[ELBO(x;\theta,\phi) \\ = \mathbb{E}_{q_\phi(y|x)}[\log {p_\theta(y)\over q_\phi(y|x)}] + \mathbb{E}_{q_\phi(y|x)} \mathbb{E}_{q_\phi(z|x,y)}(\log {p_\theta(z)\over q_\phi(z|x,y)}+\log p_\theta(x|z,y)) \\ = -[D_{KL}(q_\phi(y|x)||p_\theta(y)) + E_{q_\phi(y|x)}D_{KL}(q_\phi(z|x,y)||p_\theta(z))) + E_{q_\phi(y,z|x)}(-\log p_\theta(x|z,y))]\]Performance
Using supervised learning for classification ( not use unlabeled data)
********************************************************************************
CLASSIFICATION EVALUATION ON ENTIRE TEST SET
********************************************************************************
Test set classification accuracy: 0.7529000043869019
Using semi-supervised for classification
{'cw': 100,
'gw': 1,
'iter_max': 50000,
'iter_save': 10000,
'run': 0,
'train': 0}
Model name: model=ssvae_gw=001_cw=100_run=0000
Loaded from checkpoints/model=ssvae_gw=001_cw=100_run=0000/model-50000.pt
********************************************************************************
CLASSIFICATION EVALUATION ON ENTIRE TEST SET
********************************************************************************
Test set classification accuracy: 0.9491000175476074
Using semi-supervised to generate images based on the request
![visualize_200_digit_ssvae_[4].png](/img/posts/smvae/visualize_200_digit_ssvae_4.png)
